Transformer架构火起来以后，LayerNorm一直为人们所津津乐道，它和它的老前辈BatchNorm时常被人拿出对比。一些人为了准备面试而临时抱佛脚，把对比BatchNorm和LayerNorm的八股文背一遍。然而，网上的八股文是真的很“八股”，有些甚至是错的。所以，我要写这篇文章，尽量正确、清晰地介绍BatchNorm和LayerNorm。

协变量漂移

一切都要从独立同分布说起。众所周知，在机器学习领域，如果所有样本都由同一个分布产生，且样本之间相互独立，我们就说这些样本独立同分布。如果所有训练样本和测试样本都满足独立同分布，那么，利用训练样本做参数估计得到的分布参数同样适用于测试样本。这样，训练过程才能迅速收敛，模型才能正确预测。

当我们训练一个深度神经网络，实际上就是在用训练样本估计分布参数。然而，神经网络具有层级结构，前一层网络的输出相当于后一层网络的输入。用梯度下降训练模型时，网络参数被不断更新。对于某一层而言，前一层的网络参数一旦发生变化，它的输入分布也会相应改变。这个现象就叫协变量漂移（Covariate Shift）。

谁是协变量？顾名思义，除了第一层网络的输入是自变量以外，其他每层网络的输入都是协变量。由于这些协变量位于网络结构的内部层级，因此这个现象又叫内部协变量漂移（Internal Covariate Shift）。训练时，每个batch都会更新一次网络参数。网络层数越深，漂移现象越明显，在batch之间不断调整参数以适应不同的协变量分布，导致网络难以收敛。

梯度消失

除了协变量漂移，梯度消失的现象也会影响网络收敛。说到梯度消失，就不得不提到一个概念：饱和非线性函数（Saturating Non-linearity）。众所周知，在神经网络中，我们常用非线性函数作为激活函数。如果一个非线性函数\(f\)满足如下条件：

\[(\lvert \lim_{x\to -\infty} f(x) \rvert =+\infty)\vee (\lvert \lim_{x\to +\infty} f(x) \rvert =+\infty)\]

我们就称其为不饱和非线性函数。相反，则称其为饱和非线性函数。可以看出，饱和非线性函数总是会把输入压缩到一个较小的范围内。例如，sigmoid是饱和的，它会把输入输入\(x\)压缩到(0, 1)区间：

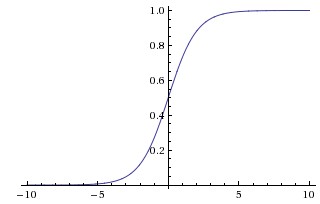
sigmoid

tanh也是饱和的，它会把输入\(x\)压缩到(-1, 1)区间：

tanh

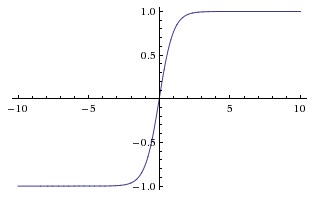
ReLU是不饱和的，随着输入\(x\)增加，它也趋于无穷大：

relu

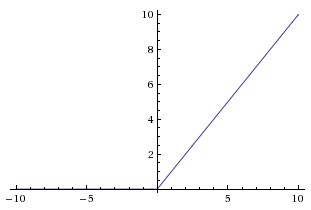
饱和非线性函数有个不好的性质：存在大片导数趋于0的饱和区域。反向传播时，如果网络某一层的激活函数的输入正好处于饱和区域，由于计算这一层的权重梯度时需要乘以该层激活函数的导数，因此权重梯度也会变得很小。网络越深，乘法次数越多，梯度就越小，最终导致梯度消失现象，网络收敛速度受到严重影响。

BatchNorm

于是，Sergey Ioffe等人在2015年提出了Batch Normalization。计算每个batch内部在每个维度上的均值和方差，对输入的每个维度做归一化：

batchnorm-algo

归一化后，每个batch产生的协变量在同一维度上均值都是0，方差都是1。如果协变量服从高斯分布，那么，BatchNorm把每个batch产生的协变量都归一化为标准高斯分布，做到了协变量在batch之间同分布。不仅如此，归一化把分散的样本收拢到更小的范围内，使大量样本离开非线性激活函数的饱和区域，梯度消失问题得到缓解。

然而，看似简单的算法，背后总是有些问题让人困惑。

  • 归一化得到的\(\hat{x}_i\)没有直接输出，真正的输出是\(\gamma \hat{x}_i+\beta\)。为什么要这么做呢？

因为每层的输入被归一化之后，会影响这一层本来的表示能力。为了保证每一层仍然具备原有的表示能力，引入两个可学习的变量\(\gamma\)和\(\beta\)。对于某一层网络，令\(x^{(k)}\)表示输入的第\(k\)个维度的值，归一化之后，得到\(\hat{x}^{(k)}\)：

\[\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}\]

当\(\gamma=\sqrt{Var[x^{(k)}]}, \beta=E[x^{(k)}]\)时，\(\gamma \hat{x}^{(k)}+\beta\)可以还原\(x^{(k)}\)。

  • 为什么不用整个训练集的数据计算均值和方差？

因为每个batch都会更新网络参数，如果你想使用整个训练集的均值和方差，每次参数更新后，都要先把整个训练集输入网络，计算每一层的输出，然后根据每层的输出求出均值和方差，再把下一个batch输入网络，用刚才求出的均值和方差做归一化，计算量很大。相反，计算一个batch的均值和方差，却可以在这个batch的前向传播过程中一并完成。这里的假设是每个batch的统计量都是全体训练样本的一个估计。理论上，batch越大，估计越准。

  • 训练时的BatchNorm解决了，但是，测试时没有batch可供计算统计量，如何做BatchNorm呢？

测试阶段的BatchNorm用的是训练阶段的统计量。训练时，每个BatchNorm层都会存储均值和方差。设当前batch的均值和方差分别是mean和var，动态计算均值running_mean和方差running_var的公式如下：

running_mean = momentum * running_mean + (1 - momentum) * mean
running_var = momentum * running_var + (1 - momentum) * var

momentum用于调节当前batch的统计量和动态统计量的权重。当momentum=0时,测试阶段使用的统计量就是训练时最后一个batch的统计量，当momentum=1时，测试阶段使用的统计量就是基于所有训练batch计算出的动态统计量。因此，大部分情况下都会让momentum接近1,这样可以让测试阶段的统计量更接近真实情况。

计算动态统计量的方法可以参考Pytorch对BatchNorm的C++实现：

      if (running_mean.defined()) {
        running_mean_a[f] = momentum * mean + (1 - momentum) * running_mean_a[f];
      }
      if (running_var.defined()) {
        accscalar_t unbiased_var = var_sum / (n - 1);
        running_var_a[f] = momentum * unbiased_var + (1 - momentum) * running_var_a[f];
      }

LayerNorm

2016年，Jimmy Lei Ba等人提出LayerNorm。经过上文对BatchNorm的铺垫，LayerNorm显得更简单了。既然想让每层输出（即下一层的输入）都有相同分布，为什么不直接对每层的输出做归一化呢？尤其对于ReLU这样的不饱和激活函数，它的输出变化范围很大，对它的输出做归一化，可以把它的输出收拢到一个较小范围内，稳定输出分布的效果非常明显。

对于网络的第\(l\)层，令\(H\)表示该层的神经元数量，\(a_i^l\)表示该层第\(i\)个神经元的输出，则该层的均值\(\mu^l\)和方差\(\sigma^l\)计算公式为：

\[\mu^l=\frac{1}{H}\sum\limits_{i=1}^{H}a_i^l\] \[\sigma^l=\sqrt{\frac{1}{H}\sum\limits_{i=1}^{H}(a_i^l-\mu^l)^2}\]

归一化后，每层的输出为：

\[h_{i}=f(\frac{g_{i}}{\sigma_{i}}(a_{i}-\mu_{i})+b_{i})\]

其中，f是激活函数，增益\(g_{i}\)和偏置\(b_{i}\)是需要学习的两个参数。

LayerNorm具有良好的re-centering和re-scaling不变性。所谓re-centering就是用减均值的方式实现均值为0的效果，re-scaling就是用除以方差的方式实现缩放效果。re-centering不变性使模型对输入和权重漂移不敏感，re-scaling不变性使模型的输出不会受到输入和权重随机缩放的影响。

可见，与BatchNorm计算batch内所有样本在各维度上的均值和方差不同，LayerNorm直接计算每一层输出的均值和方差。对BatchNorm而言，batch size会影响均值和方差的计算。但是，LayerNorm对batch size不敏感，这也它对BatchNorm的一个重要优势。

形象的对比

这里借用两篇论文中的插图，对BatchNorm和LayNorm做一个形象的对比。第一篇论文用下图展示了BatchNorm和LayerNorm的不同：

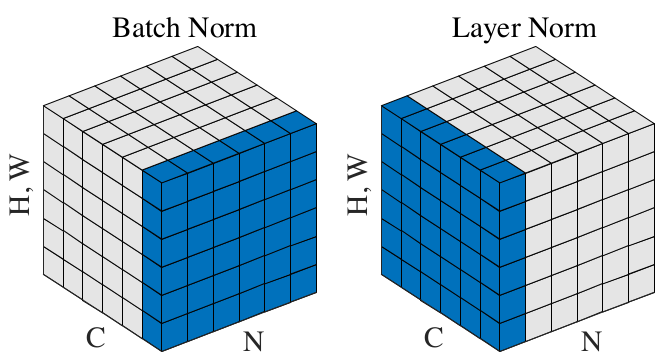
batchnorm-layernorm-1

蓝色表示归一化的对象。N是batch维度，C是channel维度。对于图像，每个channel都可以看作一个特征维度。按照上图，BatchNorm显然是对一个batch内所有样本的某个channel做归一化，而LayerNorm对某一个样本的所有channel做归一化。

上图是从处理图像的角度对比二者的区别。第二篇论文则从处理文本的角度做了对比：

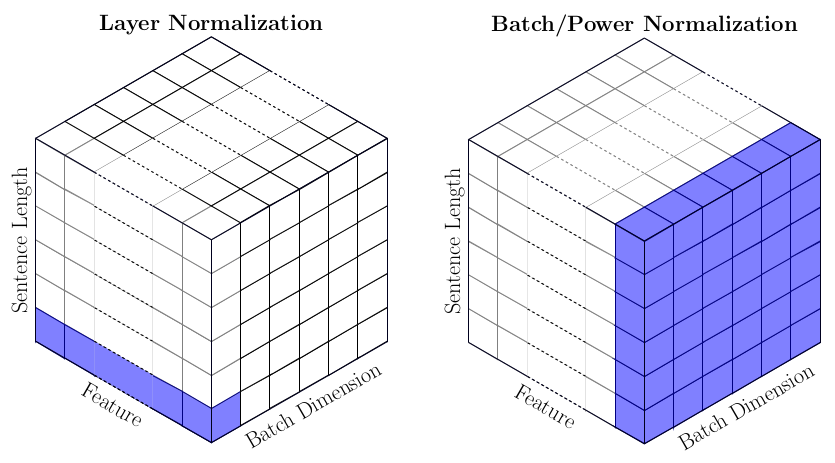
batchnorm-layernorm-2

蓝色表示归一化的对象。BatchNorm与上一幅图基本一致，对一个batch内所有样本的某一个特征维度做归一化。但是，LayerNorm与上一幅图有所不同，这里是对某一个样本的某一个token的所有特征维度（即该token的embedding）做归一化。在Transformer结构中，每个token都是单独的语义单元。LayerNorm的作用是让每层语义单元的输出分布保持稳定。

最后，希望每个算法工程师都能脚踏实地，夯实基础。八股文害人不浅，在我看来，面试时问八股文甚至不如和候选人直接聊家常，更能体现候选人的品质和沟通能力。如果面试官只聊八股，问不出有深度有细节的问题，那最好尽快结束面试，不要浪费彼此的时间。

明天一早要驱车300公里到浙江徒步，就写到这里了。