在这篇文章中，我介绍了适配器方法，用于实现大模型的参数高效微调。2021年，E. Hu等人提出了一种新的适配方法，称为Low-Rank Adaption (LoRA)，即“低秩适配”，同样实现了预训练模型的参数高效微调，且不会增加模型的推理延迟。

内在维度

LoRA受到预训练模型存在“内在维度”现象的启发。为了理解“内在维度”，首先思考一个问题：预训练模型往往拥有数十亿甚至更多参数，为何适配到下游任务时只需要数百至数千的样本就能微调？

2020年，A. Aghajanyan等人研究了这一现象，发现预训练模型存在一个较低的“内在维度”，使用少量样本微调时，实际上是在更新低维空间中的参数。把预训练模型的全部参数看成一个D维参数向量，记为\(\theta^{(D)}\)，模型的原始参数为\(\theta_{0}^{(D)}\)，设\(\theta^{(d)}\)是d维子空间中的一个向量，d<D，利用一个固定的D*d映射矩阵P把d维空间中的向量映射到D维空间，\(\theta^{(D)}\)可写为：

$$ \theta^{(D)}=\theta_{0}^{(D)} + P\theta^{(d)} $$

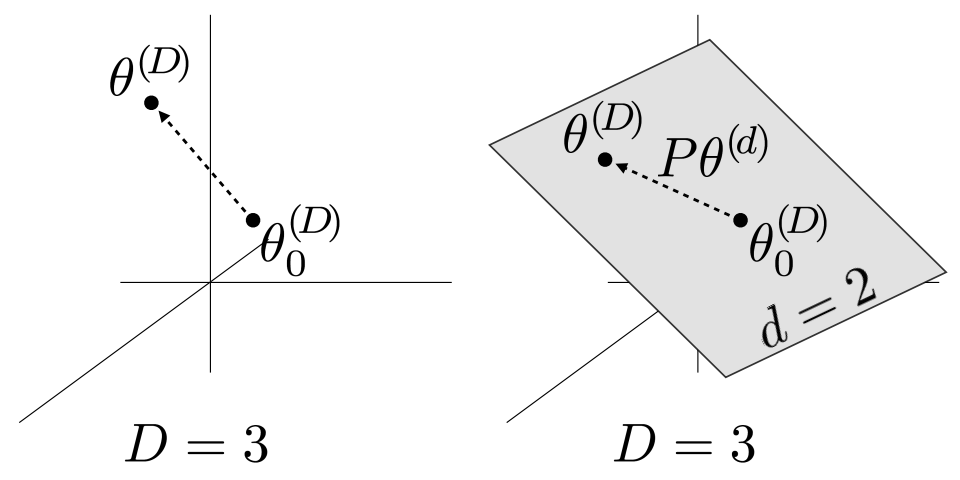
下图中，以D=3，d=2为例：

intrinsic-dimension-D3-d2

左图直接在3维空间中训练模型，直接优化原始模型参数\(\theta_{0}^{(D)}\)，把它更新为\(\theta^{(D)}\)。右图冻结\(\theta_{0}^{(D)}\)，转而在2维空间中寻找一个\(\theta^{(d)}\)，再用矩阵P把\(\theta^{(d)}\)映射到3维空间。如果用右图的方式可以把模型优化到良好的效果，例如，达到了全量参数微调效果的90%，则该模型的内在维度\(d_{90}=2\)。

实验表明，仅训练200个参数，就可以使RoBERTa-large在MRPC数据集上的效果达到全量参数微调效果的90%。

低秩适配

预训练模型的权重矩阵通常具有满秩，这意味着权重矩阵的各个列向量之间线性无关，这样的矩阵没有冗余信息，是无法被压缩的。但是，“内在维度”现象表明，微调模型时只需更新少量参数，这启发我们微调时产生的权重增量矩阵\(\Delta W\)可能包含大量冗余参数，\(\Delta W\)很可能不是满秩的。对低秩矩阵做分解，可以利用较少的参数重建或近似原矩阵。这就是LoRA的核心思想。

设输入为x，微调时得到增量\(\Delta W\)，与原始权重\(W_{0}\)相加得到更新后的权重，输出\(h=(W_{0} + \Delta W)x\)。根据矩阵的乘法分配律，有\(h=W_{0}x+\Delta Wx\)，这意味着微调时可以保持\(W_{0}\)不变，分别将\(W_{0}\)、\(\Delta W\)与x相乘，最后把两个乘积相加即可得到输出h。

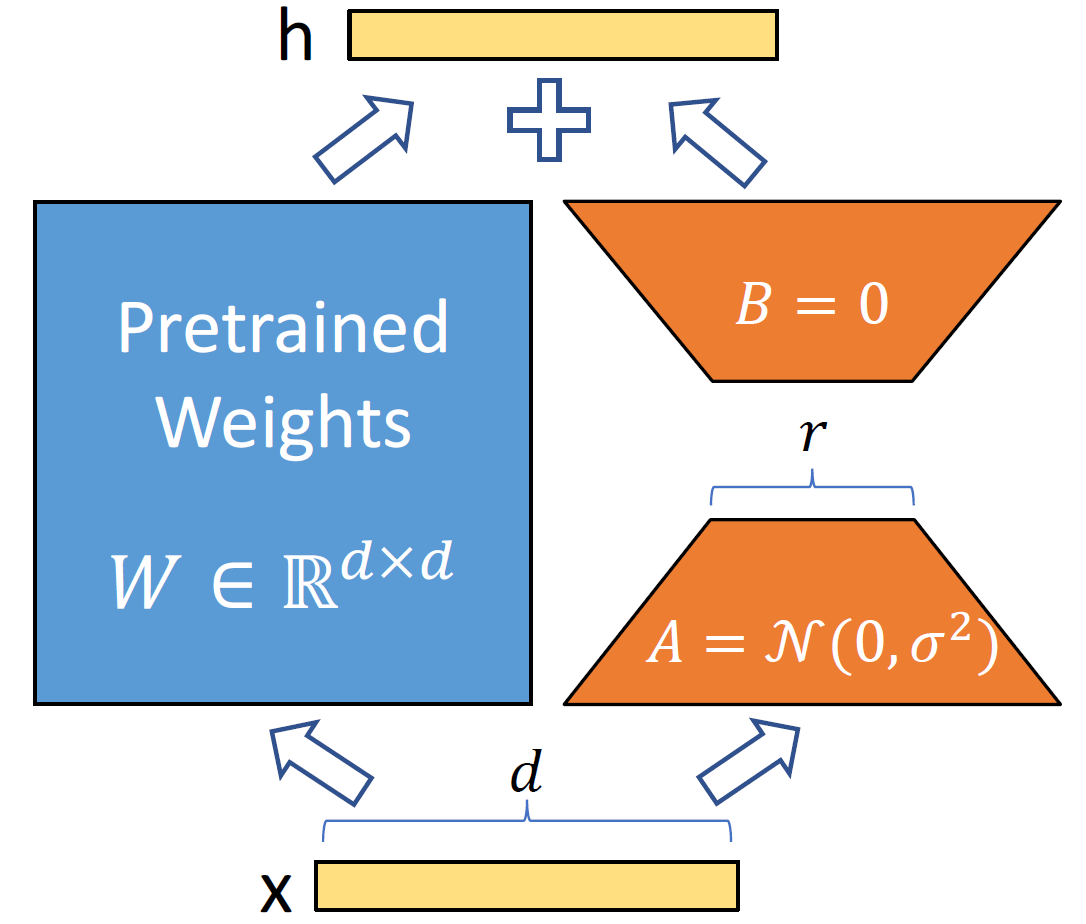
设\(W_{0}\in\mathbb{R}^{d\times k}\)，\(\Delta W\)的秩为r，\(\Delta W=BA\)是\(\Delta W\)的一个满秩分解，其中\(B\in\mathbb{R}^{d\times r}, A\in\mathbb{R}^{r\times k}, r\ll min(d, k)\)。训练时，分别用随机高斯和零矩阵初始化A和B，确保初始化时BA是零矩阵，对模型效果没有影响。训练过程中冻结\(W_{0}\)，只更新矩阵B和A，共r(d+k)个参数，从而实现“参数高效”微调。推理时，分别计算\(W_{0}x\)和 \(BAx\)并相加，得到输出h，如下图所示：

reparameterization-of-lora

实际上，r是一个超参，训练时可任意设定，\(\Delta W\)真正的秩未必等于r。如果r恰好等于\(\Delta W\)的秩，甚至大于\(\Delta\)的秩（例如等于预训练权重矩阵\(W_{0}\)的秩），利用学到的B和A可以完全重建\(\Delta W\)，这时，LoRA的效果近似于全量微调。如果r小于\(\Delta W\)的秩，BA就是\(\Delta W\)的一个低秩近似，利用矩阵B和A可以恢复矩阵\(\Delta W\)中的部分信息。

使用方法

论文提供了代码，使用非常方便。只需用LoRA提供的包含低秩分解的层替换原模型的层即可，例如：

# ===== Before =====
# layer = nn.Linear(in_features, out_features)

# ===== After ======
import loralib as lora
# Add a pair of low-rank adaptation matrices with rank r=16
layer = lora.Linear(in_features, out_features, r=16)

保存checkpoint时，只保存低秩分解的矩阵参数：

# ===== Before =====
# torch.save(model.state_dict(), checkpoint_path)
# ===== After =====
torch.save(lora.lora_state_dict(model), checkpoint_path)

加载checkpoint时，预训练权重矩阵和LoRA权重矩阵分开加载：

# Load the pretrained checkpoint first
model.load_state_dict(torch.load('ckpt_pretrained.pt'), strict=False)
# Then load the LoRA checkpoint
model.load_state_dict(torch.load('ckpt_lora.pt'), strict=False)

优势明显

在线部署时，只需保存一份\(W_{0}\)以及适配不同任务的矩阵B和A。在不同任务间切换时，只需取得不同任务的B和A，与\(W_{0}\)相加，得到最终的权重矩阵\(W=W_{0}+BA\)。与普通的适配器方法相比，LoRA没有增加网络深度，因此不会增加推理延迟。

使用Adam训练Transformer时，由于不需要保存被冻结的\(W_{0}\)的优化器状态，显存占用减少2/3。微调GPT-3 175B时，所需显存从1.2T减少到350G。当r=4且只适配Q和V矩阵时，训练得到的checkpoint从350G减小到35M。由于冻结了大部分参数，不必计算它们的梯度，训练GPT-3 175B的速度提升了25%。

适配哪些矩阵

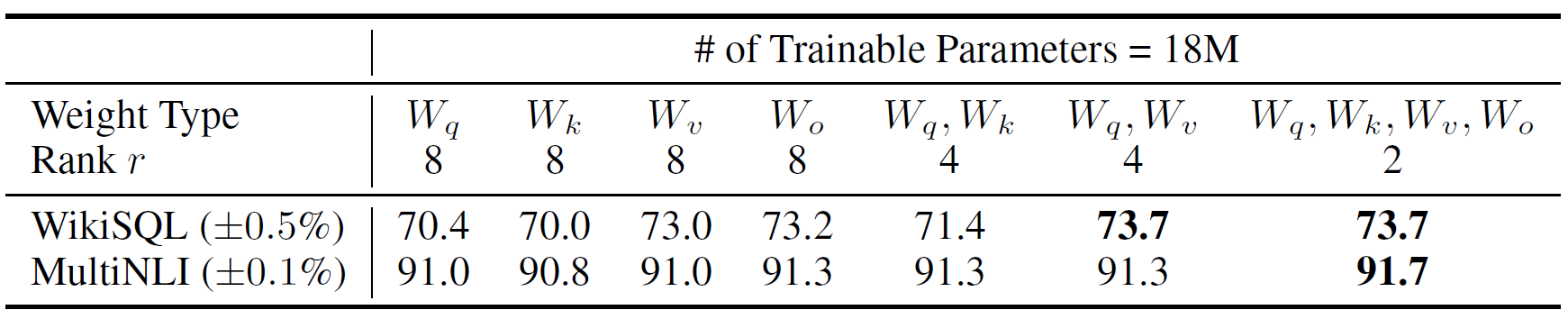
以微调GPT-3 175B为例，共96层，模型输入维度为12288，分为96个头。当r=8时，只适配注意力矩阵中的某一种，即Q、K、V或多头输出拼接之后经过的变换矩阵O，一层LoRA的参数量为\(r(d+k)=8(12288 + 12288)=196608\)，96层的参数总量为\(96*196608=18874368\approx 18M\)。如果保持参数量不变，当r=4时，可以同时适配Q、K、V、O中的两种。在WikiSQL和MultiNLI两个数据集上的效果如下：

accuracy-of-lora-on-different-types-of-attention-weights

可见，在同等参数量的情况下，同时适配两个矩阵的效果由于只适配单一矩阵，同时适配Q和V效果最好。

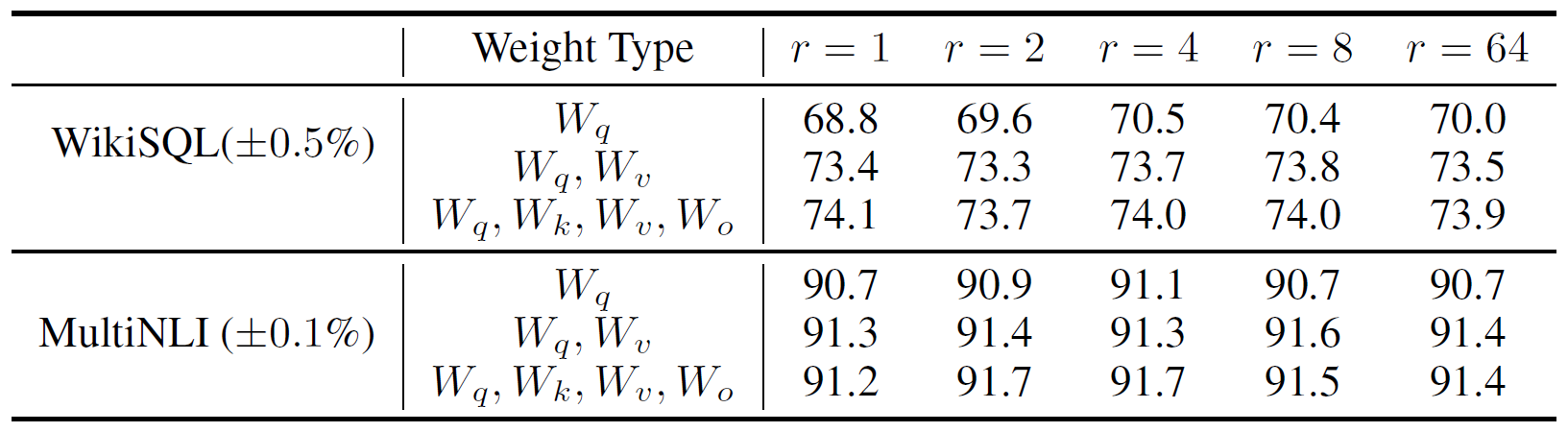
怎样选择秩

从下面的实验结果可以看出，只适配Q矩阵时，需要的r相对较大。但是，同时适配Q和V矩阵时，很小的r，甚至r=1时，即可实现较好的效果。这说明\(\Delta W\)可能具有很小的内在秩。

accuracy-of-lora-with-different-rank

为了解释这一现象，猜想对于不同的r，学到的不同子空间之间具有较高的相似度，增大r并不能得到一个更有意义的子空间。以矩阵A为例，对于同一个预训练模型，r=8和r=64时，学到的A分别记为\(A_{r=8}\)和\(A_{r=64}\)。如果\(A_{r=8}\)和\(A_{r=64}\)所在的两个子空间具有较高相似度，那么，这两个子空间也具备相似的表示能力，\(A_{r=8}\)和\(A_{r=64}\)作为这两个子空间中的两个向量，产生的效果也会比较相似。

如何计算这两个子空间的相似度？如果能找到张成两个子空间的规范正交基，就可以利用投影度量计算它们张成的子空间之间的相似度。如何找到\(A_{r=8}\)和\(A_{r=64}\)所在子空间的规范正交基？奇异值分解SVD是一种常用方法，分解后得到的右酉矩阵（在实数范围内就是规范正交阵）的列向量构成了一组规范正交基，可以认为这组规范正交基张成了一个线性子空间，原矩阵就是该空间中的一个向量。

设\(A_{r=8}\)和\(A_{r=64}\)经过SVD分解后的右酉矩阵分别是\(U_{A_{r=8}}\)和\(U_{A_{r=64}}\)，我们把\(U_{A_{r=8}}\)的前i个列向量记为\(U_{A_{r=8}}^{i}\), 其中\(i\in [1,8]\)，把\(U_{A_{r=64}}\)的前j个列向量记为\(U_{A_{r=64}}^{j}\)，其中 \(j\in [1, 64]\)。\(U_{A_{r=8}}^{i}\)和\(U_{A_{r=64}}^{j}\)各自张成子空间，为了计算它们之间的相似度，设\(\left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j}\)奇异值为\(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{p}\)，其中\(p=\min(i, j)\)，用投影度量计算两个子空间之间的距离：

$$ d\left (U_{A_{r=8}}^{i}, U_{A_{r=64}}^{j}\right )=\sqrt{p-\sum_{i=1}^{p}\sigma_{i}^{2}} $$

当\(U_{A_{r=8}}^{i}\)和\(U_{A_{r=64}}^{j}\)相等时，由于它们各自的列向量都规范且正交，所以\(\left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j}\)是一个单位阵，单位阵的奇异值均为1，这时，d取最小值0。当\(U_{A_{r=8}}^{i}\)张成的子空间和\(U_{A_{r=64}}^{j}\)张成的子空间正交时，\(\left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j}\)是零矩阵，零矩阵的奇异值均为0，这时，d取最大值\(\sqrt{p}\)。

LoRA论文中按照如下定义计算两个子空间的规范化相似度：

$$ \phi(A_{r=8}, A_{r=64}, i, j)=\frac{\left\| \left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j} \right\|_{F}^{2}}{\min(i,j)} $$

实际上，这一定义方式与投影度量距离是等价的。由于矩阵F范数的平方等于矩阵奇异值的平方和，上式可以写为：

$$ \phi(A_{r=8}, A_{r=64}, i, j)=\frac{\left\| \left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j} \right\|_{F}^{2}}{\min(i,j)}=\frac{\sum_{i}^{p}\sigma_{i}^{2}}{\min(i,j)} $$

把投影度量距离公式代入上式，得到：

$$ \phi(A_{r=8}, A_{r=64}, i, j)=\frac{\left\| \left (U_{A_{r=8}}^{i} \right )^{T}U_{A_{r=64}}^{j} \right\|_{F}^{2}}{\min(i,j)}=\frac{\sum_{i}^{p}\sigma_{i}^{2}}{\min(i,j)}=\frac{p-d\left (U_{A_{r=8}}^{i}, U_{A_{r=64}}^{j}\right )}{p} $$

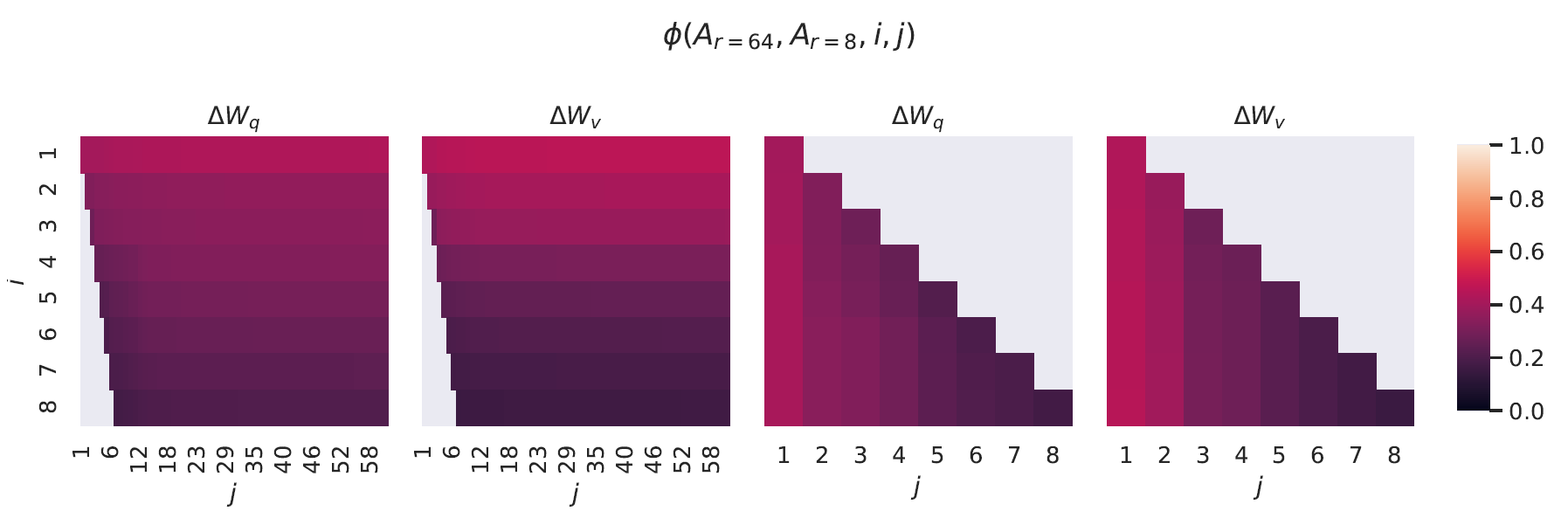
可见，基于F范数的相似度与基于投影度量的距离具有内在的等价性：距离越大，相似度越低，反之亦然，最大距离对应的相似度为0，最小距离对应的相似度为1。分别考察GPT-3 175B第48层的Q和V，分别计算\(U_{A_{r=8}}^{i}\)和\(U_{A_{r=64}}^{j}\)张成的子空间相似度：

subspace-similarity-r8-r64-for-q-v

右边两图是左边两图左下角的放大。从左边两图可以看出，当i=1时，\(U_{A_{r=8}}\)和\(U_{A_{r=64}}\)张成的子空间相似度已超过0.5。随着i不断增大，它们张成的子空间相似度反而降低。这说明两个空间的相似性主要体现在第一个奇异向量对应的方向上。从右边两图可以看出类似的结论，当j=1时，\(U_{A_{r=8}}\)和\(U_{A_{r=64}}\)张成的子空间相似度最高。不同的r对应了不同的A矩阵，但是每个A矩阵所在的子空间中，第一个奇异向量对应的方向是最重要的，因此，r=1已经可以捕获最重要的信息。

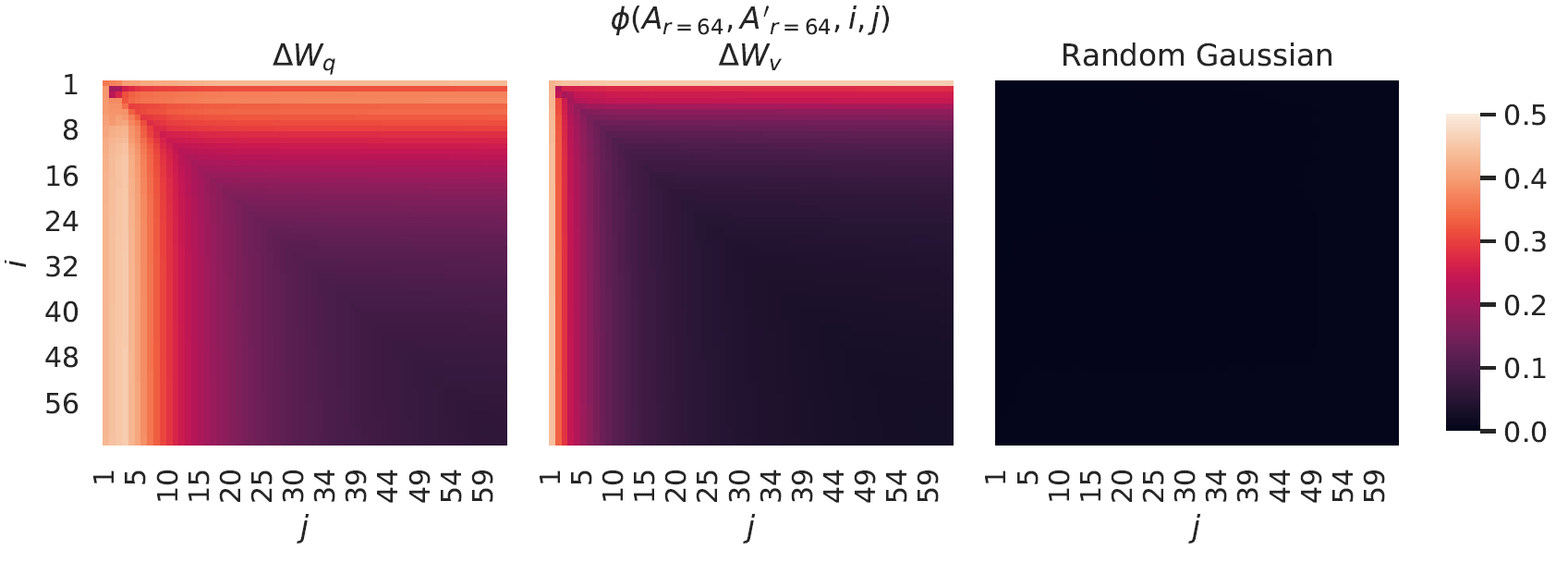
从上面的分析可以看出，对于不同的r，第一个奇异向量对应的方向最重要。那么，对于同一个r，用不同的种子初始化并训练得到不同的矩阵A，结论是怎样的？下图展示了r=64时，用两个不同种子初始化训练得到的A对应子空间相似度的情况：

subspace-similarity-r64-two-seeds-for-q-v

从图上可以看出，A和A’各自所在子空间的正交基的第一个向量张成的子空间的相似度是最高的，超过0.5。作为对比，最右图用随机高斯初始化两个矩阵，并计算它们各自所在的子空间的正交基张成子空间的相似度，几乎为0。这说明A和A’各自所在子空间具有相似性并非偶然现象。