大模型的温度
大模型 调用大模型接口时,往往有一个可选的temperature参数。例如,百度千帆的Yi-34B模型API文档对temperature的解释为:
(1)较高的数值会使输出更加随机,而较低的数值会使其更加集中和确定
(2)范围 (0, 1.0],不能为0
阿里灵积的通义千问模型API文档对temperature的解释为:
用于控制随机性和多样性的程度。具体来说,temperature值控制了生成文本时对每个候选词的概率分布进行平滑的程度。较高的temperature值会降低概率分布的峰值,使得更多的低概率词被选择,生成结果更加多样化;而较低的temperature值则会增强概率分布的峰值,使得高概率词更容易被选择,生成结果更加确定。
取值范围: [0, 2),不建议取值为0,无意义。
那么,大模型的temperature(即温度)究竟是什么?一切要从文本生成说起…
温度的本质
文本生成任务定义为:给定m个token的上文\(x_{1}, \dots, x_{m}\),生成连续n个token的下文,得到一个完整的序列\(x_{1}, \dots, x_{m+n}\)。这个序列的概率为
$$ P(x_{1:m+n})=\prod\limits_{i=1}^{m+n}P(x_{i}\mid x_{1}, \dots, x_{i-1}) $$
如果直接按照模型输出的分布选择下一个token,生成的下文序列就会非常随机,甚至和上文毫无关联。直观上,我们应该找到一个使\(P(x_{1:m+n})\)最大的token序列,或许这才是最可信的序列。现在的问题是,如何找到这个序列?
贪心搜索
Greedy search是最容易想到的一个方法:在解码的每一个时间步,都选择当前概率最大的token作为输出。假设词表为\(V=\{ yes, ok, \langle s\rangle \}\),按照下图所示的搜索树,贪心法解码得到的序列为“yes yes EOS”,该序列对应的概率为\(P=0.5\cdot 0.4\cdot 1.0=0.2\):
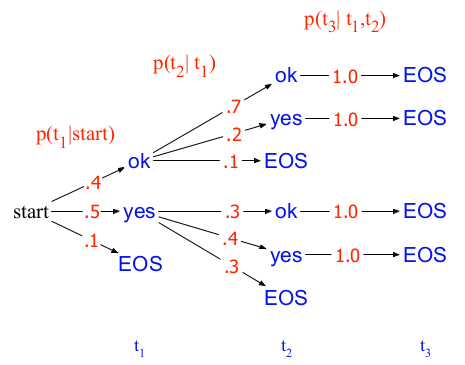
但是,上图可以解码得到的最大概率序列实际上是”ok ok EOS”,概率为\(P=0.4\cdot 0.7\cdot 1.0=0.28\)。可见,贪心法无法保证找到全局最优解。
束搜索
Beam search是最常见的搜索最大概率文本序列的方法。与贪心法每次选择一个概率最大的token不同,束搜索每次保留前k个概率最大的token,k称为束的宽度(beam width)。当k=1时,beam search退化为greedy search。
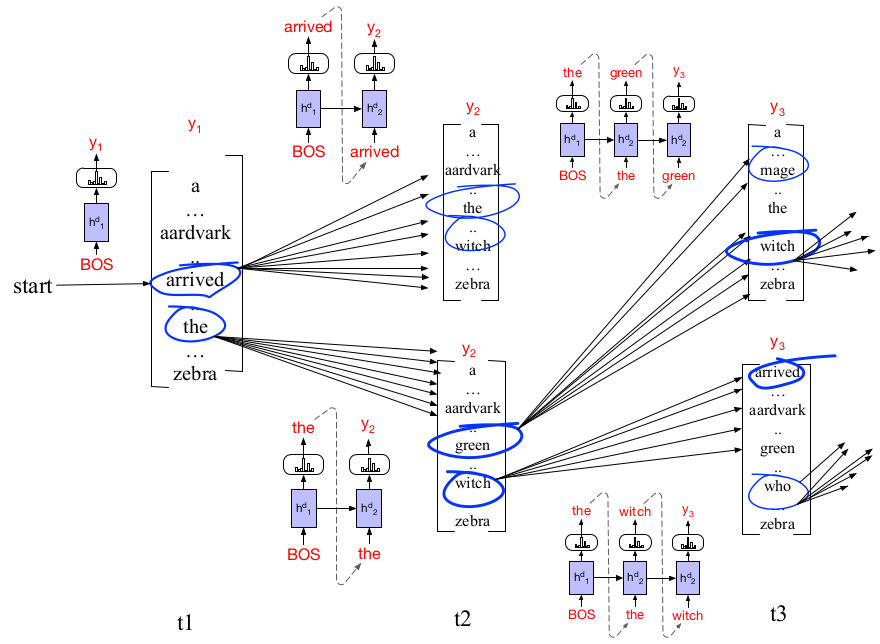
上图中,k=2。第一个时间步,保留概率最大的2个token,分别是arrived和the。第二个时间步,把arrived和the分别输入模型,各得到一个分布:arrived得到的分布中,保留概率最大的2个token,分别是the和witch;the得到的分布中,保留概率最大的2个token,分别是green和witch。至此,我们得到4个序列:arrived the, arrived witch, the green, the witch。从这4个序列中选择2个概率最大的,进入第三个时间步。依此类推,直到有一个序列输出EOS,就把该序列从搜索树中移除,同时,束宽度减1。直到束宽度减为0,搜索结束。
核采样
与greedy search一样,beam search的目标仍是搜索概率最大的序列。但是,概率最大的序列一定是最好的序列吗?2019年,Holtzman等人在论文中指出,如果以输出最大概率序列为解码目标,即使是当时最强大的GPT-2,生成的文本也会出现退化,例如输出重复内容。
下图中,给定一个上文,用模型生成下文,beam search搜索到的序列的概率始终处于高位,而人工生成序列的概率则高低起伏。这说明概率最大的序列未必是最接近人类表达习惯的序列,真正的人类表达充满多样性,正如下图的标题所说:Beam search text is less surprising。
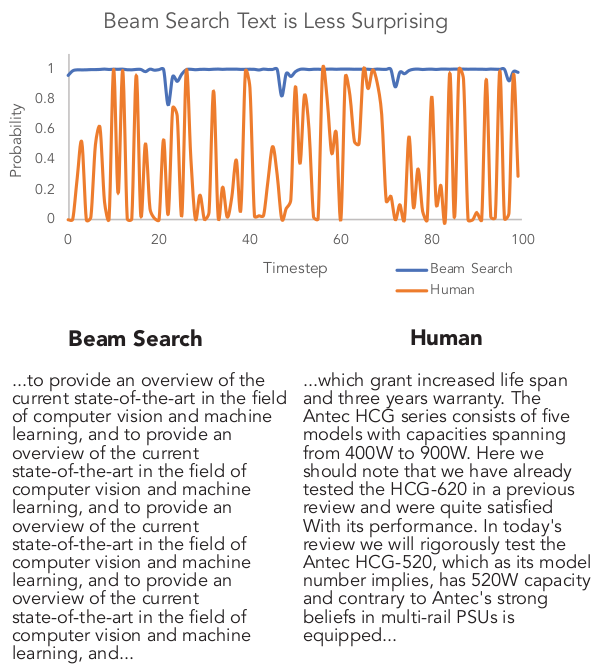
那么,如何使生成文本摆脱普通、重复的陷阱,使之具有更丰富的变化和多样性呢?根据上面的分析,我们既不能完全按照模型输出的分布采样得到一个完全随机的序列,也不能像beam search那样寻找最大概率得到一个缺乏创造性的序列。真正符合人类表达习惯的序列应当介于这两者之间。
于是,Holtzman等人提出了nucleus samling方法,即核采样。给定一个分布\(P(x\mid x_{1:i-1})\),满足下式的最小词表\(V^{(p)}\subset V\)称为该分布的top-p词表:
$$ \sum\limits_{x\in V^{(p)}}P(x\mid x_{1:i-1})\geq p $$
核采样的关键点在于生成下一个token时只能从top-p词表中采样。令\(p'\)表示\(P(x\mid x_{1:i-1})\)的top-p词表中所有单词的概率和,即\(p'=\sum\limits_{x\in V^{(p)}}P(x\mid x_{1:i-1})\),把这些概率归一化,得到新分布\(P'(x\mid x_{1:i-1})\),生成下一个token时按照新分布从top-p词表中采样:
\[P'(x\mid x_{1:i-1})= \begin{cases} \frac{P(x\mid x_{1:i-1})}{p'} & x\in V^{(p)} \\ 0 & otherwise \end{cases}\]一方面,top-p词表包含了原始词表中概率最大的若干个单词(通常为1到数千个),因此不会完全随机生成下一个token。另一方面,top-p词表在每个时间步可能都不相同,在top-p词表内部按照\(P'(x\mid x_{1:i-1})\)生成下一个token,又引入了一定的随机性。通常,p越大,top-p词表越大,原始分布的大部分概率质量都出现在这个词表中,生成文本的多样性越强。这个词表就叫做“核”(necleus)。
温度采样
经过前文的铺垫,本文主角“温度采样”终于登场。与核采样一样,温度采样也是为了增加生成文本的多样性。思路很简单,就是利用温度\(t\)调节原始概率分布。设当前时间步模型输出logits的第\(l\)个数值为\(u_{l}\),温度为\(t\),则下一个token选择词表中第\(l\)个单词\(V_{l}\)的概率为:
\[p(x=V_{l}\mid x_{1:i-1})=\frac{\exp(u_{l}/t)}{\sum\limits_{l'}\exp(u_{l'}/t)}\]可见,温度采样只是简单修改了用于计算分布的softmax函数。温度越低,token之间的概率相差越大,采样时就会越稳定地偏向于高概率token。相反,温度越高,token之间的概率相差越小,生成token的随机性(或多样性)越强。我们可以通过计算概率分布的熵感受温度带来的差异:
import torch
from torch.distributions.categorical import Categorical
logits = torch.rand(2, 5)
# [[0.6508, 0.0325, 0.9272, 0.4163, 0.8083],
# [0.8909, 0.5329, 0.7321, 0.0875, 0.8136]]
cat = Categorical(logits=logits)
ent = cat.entropy()
# [1.5663, 1.5757]
# low temperature, low entropy
low_t_logits = logits / 0.3
cat = Categorical(logits=low_t_logits)
ent = cat.entropy() # [1.3097, 1.3922]
# high temperature, high entropy
high_t_logits = logits / 2.0
cat = Categorical(logits=high_t_logits)
ent = cat.entropy() # [1.5977, 1.6000]
可见,温度越低,熵越低,说明不同token之间的概率相差较大,生成内容稳定性较好。温度越高,熵越高,说明不同token之间的概率相差较小,生成内容多样性较好。
通过调节温度,改变生成token的概率分布,这就是温度的本质。
其他应用
温度调节的方法不仅用于文本生成,类似的思想还被用在很多NLP领域。
M-BERT和XLM
前面文章介绍过一种跨语言的预训练模型M-BERT,它从Wikipedia中选取100种语言做预训练,但是每种语言的语料数量分布很不均匀,如果按照各语言所占比例采样,低资源语言就很难被采入训练语料。因此,M-BERT采用了一种“指数平滑”的采样方法,设第i种语言的语料占全部语料的比例为\(p_{i}\),该语言的语料被采样的概率为:
$$ q_{i}=\frac{p_{i}^{s}}{\sum{p_{j}^{s}}} $$
实际上,XLM也用了这种方法采样不同的语言,具体参考这篇文章。这里,s可以看作是一种“温度”,调节了原本按照样本比例采样的概率分布。
T5
2020年,T5把这个方法用于数据集采样。T5采用多任务学习方法,把无监督和有监督任务的数据集都转化成text-to-text的形式,混合在一起输入encoder-decoder架构做训练。但是,不同任务的数据集规模相差很大,例如,无监督去噪任务的数据比其他有监督任务多了几个数量级,一些有监督任务(例如英译法)的数据比其他有监督任务多得多。如果按照比例采样,有些任务的数据就很难被采到。
为了缓解这个问题,T5提出了一个方法:计算数据集规模的比例时人为设置一个数据量上限,记为\(K\),如果某个数据集的数据量超过此上限,则以\(K\)代替真实数据量。采样第m个任务数据集的概率为:
$$ r_{m}=\frac{\min(e_{m}, K)}{\sum\min(e_{n}, K)} $$
其中,\(N\)是数据集的数量,\(e_{n}\)是第n个数据集的数据量,\(n\in {1, \dots, N}\)。这个方法相当于给规模过大的数据集做截断,能有效缓解采样比例失衡的问题。这个方法整体上还是遵循了按照样本比例采样的思路,称为examples-proportional mixing。
更进一步,借鉴M-BERT采样不同语种的思路,T5提出了另一个缓解采样比例失衡问题的方法,称为temperature-scaled mixing:给每个\(r_{m}\)加上指数\(1/T\),因此,采样第m个任务数据集的概率为:
$$ r_{m}=\frac{(\min(e_{m}, K))^{\frac{1}{T}}}{\sum(\min(e_{n}, K))^{\frac{1}{T}}} $$
其中,T就是“温度”。当\(T=1\)时,这个方法退化为examples-proportional mixing。当T逐渐增大,各数据集的采样比例趋于平均。T调节了原本按照数据集规模比例采样的概率分布。